Analysis with multipliers solution 💡

Author

Centre for Research into Ecological and Environmental Modelling
University of St Andrews

Published

August 7, 2024

Solution

Analysis with multipliers

Dung survey of deer

Returning to the data described in (Marques et al., 2001), the following code loads the relevant packages and data. The perpendicular distances are measured in centimetres, effort along the transects measured in kilometres and areas in square kilometres.

library(Distance)
data(sikadeer)
conversion.factor <- convert_units("centimeter", "kilometer", "square kilometer")

Here we did not perform a comprehensive examination of fitting a detection function to the detected pellet groups, however, as a general guideline, we truncated the longest 10% perpendicular distances.

deer.df <- ds(sikadeer, key="hn", truncation="10%", convert_units = conversion.factor)
plot(deer.df)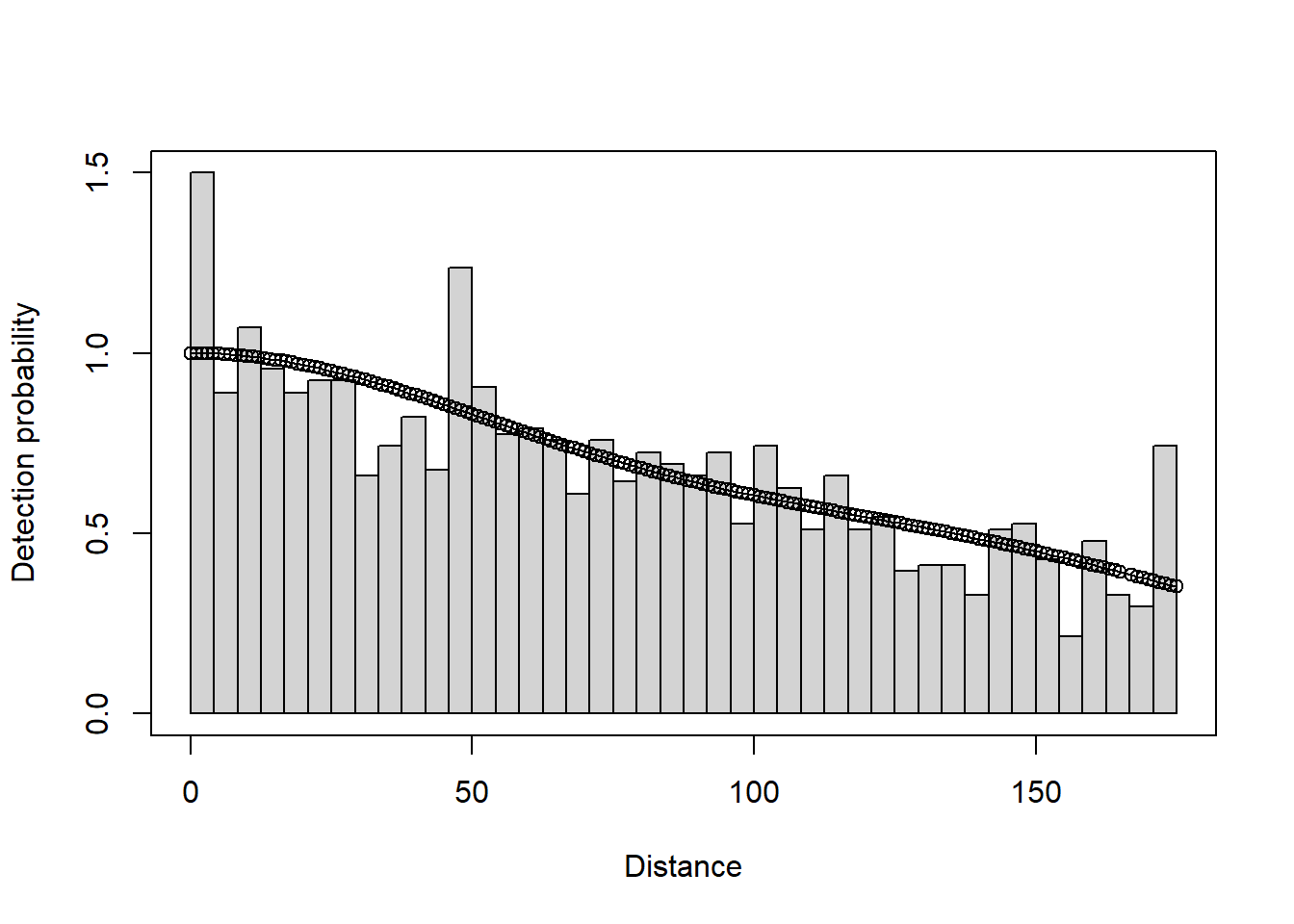

print(deer.df$dht$individuals$summary)
  Region Area CoveredArea Effort    n  k        ER      se.ER     cv.ER
1      A 13.9    0.005950   1.70 1217 13 715.88234 119.918872 0.1675120
2      B 10.3    0.003850   1.10  396 10 359.99999  86.859289 0.2412758
3      C  8.6    0.001575   0.45   17  3  37.77778   8.521202 0.2255612
4      E  8.0    0.002975   0.85   30  5  35.29412  16.568939 0.4694533
5      F 14.0    0.000700   0.20   29  1 145.00000   0.000000 0.0000000
6      G 15.2    0.001400   0.40   32  3  80.00000  39.686269 0.4960784
7      H 11.3    0.000700   0.20    3  1  15.00000   0.000000 0.0000000
8      J  9.6    0.000350   0.10    7  1  70.00000   0.000000 0.0000000
9  Total 90.9    0.017500   5.00 1731 37 201.90876   0.000000 0.0000000

The summary above shows that in blocks F, H and J there was only one transect and, as a consequence, it is not possible to calculate a variance empirically for the encounter rate in those blocks.

Estimating decay rate from data

A paper by Laing et al. (2003) describes field protocol for collecting data to estimate the mean persistence time of dung or nests to be used as multipliers. The code segment shown earlier analyses a file of such data via logistic regression to produce an estimate of mean persistence time and its associated uncertainty.

Mean persistence time                    SE                   %CV 
           163.396748             14.226998              8.707026

Using the output from calling the MIKE.persistence function, the multipliers can be specified:

# Create list of multipliers
mult <- list(creation = data.frame(rate=25, SE=0),
             decay    = data.frame(rate=163, SE=14))
print(mult)
$creation
  rate SE
1   25  0

$decay
  rate SE
1  163 14
deer_ests <- dht2(deer.df, flatfile=sikadeer, strat_formula=~Region.Label,
                  convert_units=conversion.factor, multipliers=mult, 
                  stratification="effort_sum", total_area = 100)
print(deer_ests, report="abundance")
Abundance estimates from distance sampling
Stratification : effort_sum 
Variance       : R2, n/L 
Multipliers    : creation, decay 
Sample fraction : 1 


Summary statistics:
 Region.Label  Area CoveredArea Effort    n  k      ER   se.ER cv.ER
            A  13.9    0.005950   1.70 1217 13 715.882 119.919 0.168
            B  10.3    0.003850   1.10  396 10 360.000  86.859 0.241
            C   8.6    0.001575   0.45   17  3  37.778   8.521 0.226
            E   8.0    0.002975   0.85   30  5  35.294  16.569 0.469
            F  14.0    0.000700   0.20   29  1 145.000   0.000 0.000
            G  15.2    0.001400   0.40   32  3  80.000  39.686 0.496
            H  11.3    0.000700   0.20    3  1  15.000   0.000 0.000
            J   9.6    0.000350   0.10    7  1  70.000   0.000 0.000
        Total 100.0    0.017500   5.00 1731 37 346.200  45.234 0.131

Abundance estimates:
 Region.Label Estimate      se    cv  LCI  UCI        df
            A     1027 197.474 0.192  691 1527    20.797
            B      383  99.171 0.259  220  667    11.955
            C       34   8.200 0.244   15   75     2.759
            E       29  13.959 0.479    9   99     4.329
            F      210  19.752 0.094  174  252 60314.199
            G      126  63.399 0.505   18  858     2.147
            H       18   1.649 0.094   15   21 60314.199
            J       69   6.539 0.094   58   83 60314.199
        Total     3575 575.860 0.161 2560 4990    20.215

Component percentages of variance:
 Region.Label Detection    ER Multipliers
            A      4.07 75.96       19.97
            B      2.24 86.76       10.99
            C      2.52 85.14       12.34
            E      0.66 96.13        3.22
            F     16.93  0.00       83.07
            G      0.59 96.52        2.89
            H     16.93  0.00       83.07
            J     16.93  0.00       83.07
        Total      8.09 91.91        0.00

There are a few things to notice:

  • overall estimate of density
    • most effort took place in woodland A where deer density was high. Therefore, the overall estimate is between the estimated density in woodland A and the lower densities in the other woodlands.
  • components of variance
    • we now have uncertainty associated with the encounter rate, detection function and decay rate (note there was no uncertainty associated with the production rate) and so the components of variation for all three components are provided.

In woodland A, there were 13 transects on which over 1,200 pellet groups were detected: uncertainty in the estimated density was 19% and the variance components were apportioned as detection probability 4%, encounter rate 76% and multipliers 20%.

In woodland E, there were 5 transects and 30 pellet groups resulting in a coefficient of variation (CV) of 48%: the variance components were apportioned as detection probability 0.7%, encounter rate 96% and multipliers 3%.

In woodland F only a single transect was placed and the CV of density of 9% was apportioned as detection probability 17% and multipliers 83%. Do you trust this assessment of uncertainty in the density of deer in this woodland? We are missing a component of variation because we were negligent in placing only a single transect in this woodland and so are left to ‘assume’ there is no variability in encounter rate in this woodland.

By the same token, we are left to assume there is no variability in production rates between deer because we have not included a measure of uncertainty in this facet of our analysis.

Cue counting survey of whales

data(CueCountingExample)
head(CueCountingExample, n=3)
  Region.Label  Area Sample.Label Cue.rate Cue.rate.SE Cue.rate.df object distance
1            B 85000         2.18       25           5           1     NA       NA
2            B 85000         2.19       25           5           1     NA       NA
3            B 85000         2.20       25           5           1     NA       NA
  Sample.Fraction Sample.Fraction.SE Search.time bss   sp size Study.Area
1             0.5                  0   0.1333333  NA <NA>   NA     whales
2             0.5                  0   0.1000000  NA <NA>   NA     whales
3             0.5                  0   0.4333333  NA <NA>   NA     whales
CueCountingExample$Effort <- CueCountingExample$Search.time
cuerates <- CueCountingExample[ ,c("Cue.rate", "Cue.rate.SE", "Cue.rate.df")]
cuerates <- unique(cuerates)
names(cuerates) <- c("rate", "SE", "df")
mult <- list(creation=cuerates)
print(mult)
$creation
  rate SE df
1   25  5  1

The estimated cue rate, \(\hat \nu\), is 25 cues per unit time (per hour in this case). Its standard error is 5, therefore the CV of cue rate is \(5/25 = 0.2\) (20%).

# Tidy up data by removing surplus columns
CueCountingExample[ ,c("Cue.rate", "Cue.rate.SE", "Cue.rate.df", "Sample.Fraction", 
                       "Sample.Fraction.SE")] <- list(NULL)
trunc <- 1.2
whale.df.hn <- ds(CueCountingExample, key="hn", transect="point", adjustment=NULL,
                  truncation=trunc)
whale.df.hr <- ds(CueCountingExample, key="hr", transect="point", adjustment=NULL,
                  truncation=trunc)
knitr::kable(summarize_ds_models(whale.df.hn, whale.df.hr), digits = 3)
Model Key function Formula C-vM p-value \(\hat{P_a}\) se(\(\hat{P_a}\)) \(\Delta\)AIC
Half-normal ~1 0.810 0.239 0.043 0.00
Hazard-rate ~1 0.747 0.281 0.065 3.07

Half the circle (point transect) was searched and so the sampling fraction \(\phi /2\pi = 0.5\). Therefore, \(\phi = \pi\) (\(\phi\) must be in radians).

The following commands obtain density estimates assuming no stratification (strat_formula=~1).

whale.est.hn <- dht2(whale.df.hn, flatfile=CueCountingExample, strat_formula=~1, 
                     multipliers=mult, sample_fraction=0.5)
print(whale.est.hn, report="abundance")
Abundance estimates from distance sampling
Stratification : geographical 
Variance       : P2, n/L 
Multipliers    : creation 
Sample fraction : 0.5 


Summary statistics:
 .Label   Area CoveredArea Effort  n  k    ER se.ER cv.ER
  Total 168000     82.4932  36.47 40 92 1.097 0.303 0.276

Abundance estimates:
 .Label Estimate       se    cv  LCI   UCI     df
  Total    13653 5262.964 0.385 6112 30500 13.058

Component percentages of variance:
 .Label Detection    ER Multipliers
  Total      21.7 51.38       26.92
whale.est.hr <- dht2(whale.df.hr, flatfile=CueCountingExample, strat_formula=~1, 
                     multipliers=mult, sample_fraction=0.5)
print(whale.est.hr, report="abundance")
Abundance estimates from distance sampling
Stratification : geographical 
Variance       : P2, n/L 
Multipliers    : creation 
Sample fraction : 0.5 


Summary statistics:
 .Label   Area CoveredArea Effort  n  k    ER se.ER cv.ER
  Total 168000     82.4932  36.47 40 92 1.097 0.303 0.276

Abundance estimates:
 .Label Estimate       se    cv  LCI   UCI     df
  Total    11589 4776.542 0.412 5017 26771 16.591

Component percentages of variance:
 .Label Detection    ER Multipliers
  Total     31.52 44.94       23.55

A half normal detection function was chosen and whale abundance was estimated to be 13,654 whales with a 95% confidence interval (6,112: 30,500).

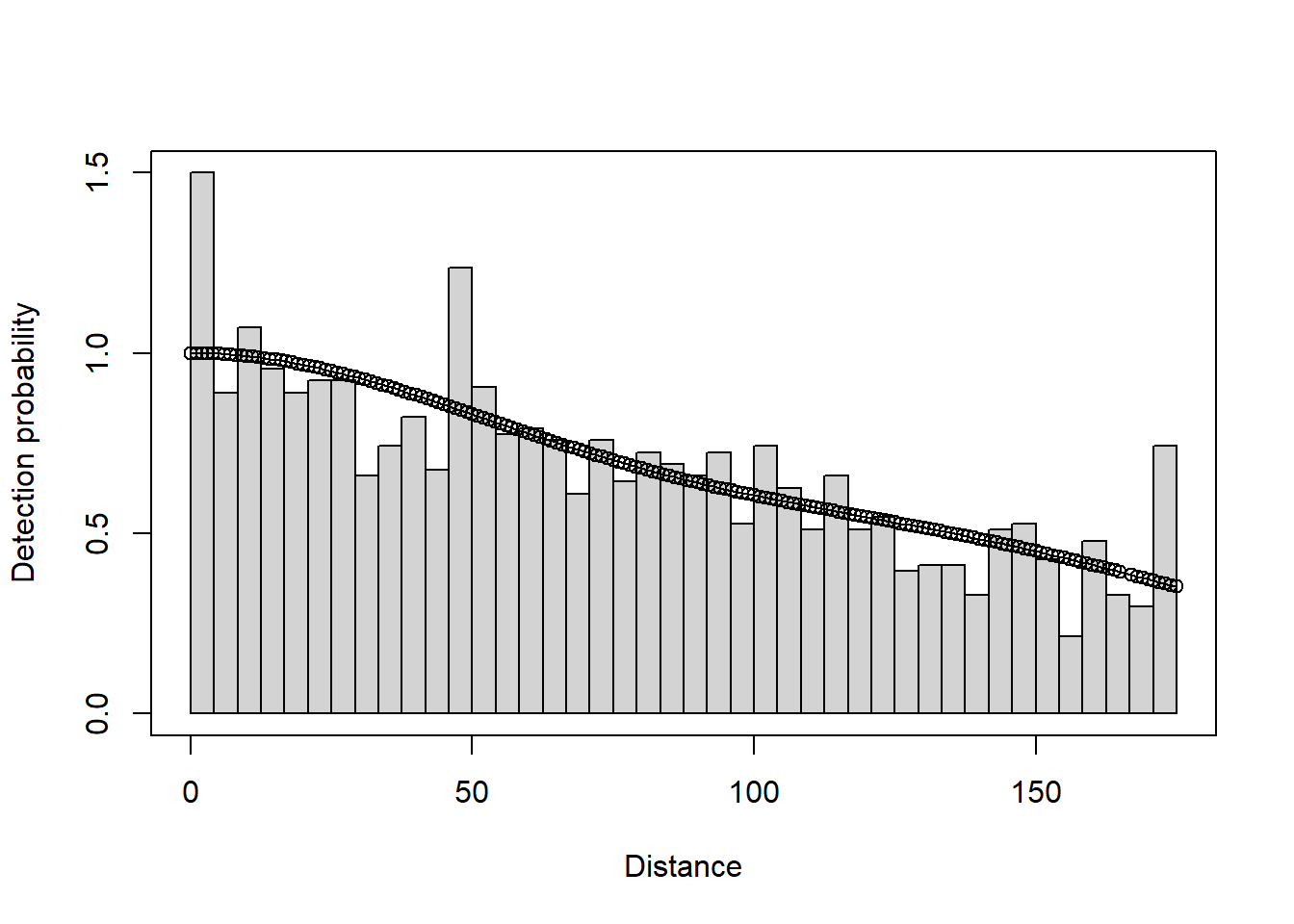
Note the large difference between the half normal estimate and the estimate from the hazard rate model, which is 11,590 whales, with 95% confidence interval (5,017; 26773). Remember that the key parameter in a cue counting analysis is \(h(0)\), the slope of the fitted pdf to the observed data at distance zero. The difference between the estimates for the different key function is the difference between these slopes for the two models (Fig. 2):

plot(whale.df.hn, pdf=TRUE, main="Half normal")
plot(whale.df.hr, pdf=TRUE, main="Hazard rate")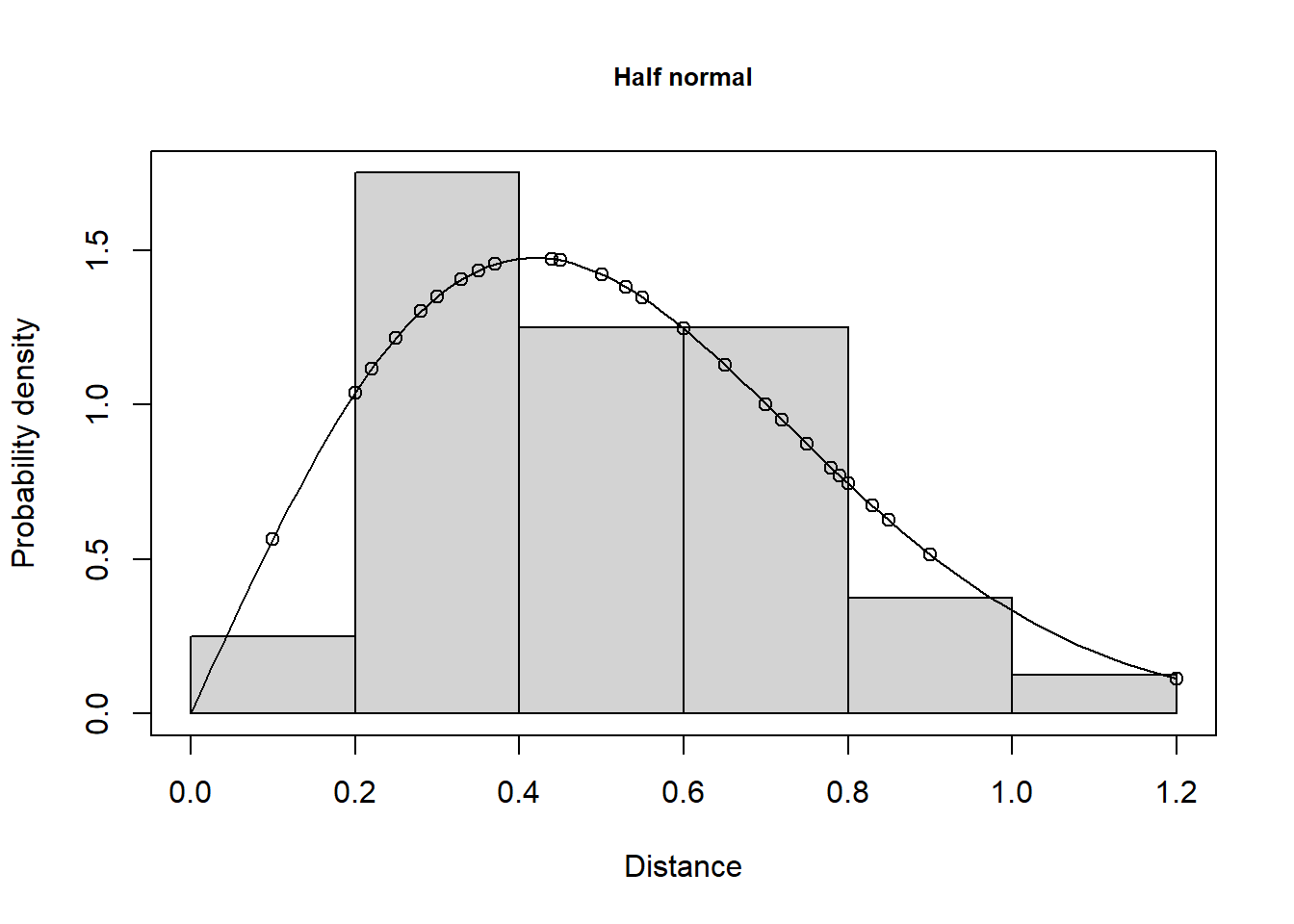

Half normal PDF

Hazard rate PDF

Cue counting estimates of detection probability are more volatile than those from line transect surveys, because on a cue counting survey you have few data where you need it most to estimate \(h(0)\) - namely at distances close to zero. As a consequence, cue-counting surveys require higher cue sample size for reliable estimation than samples of animals for line transect surveys.

Don’t worry too much about the apparent lack of fit in the first interval, or two, in Figure 2 - remember the sample size is very small in these intervals. Use the plot above and the goodness-of-fit statistics to guide you about the fit of your model.

Cue counting survey of songbirds (optional)

Analysis of the cue count data of winter wrens described by Buckland (2006).

data(wren_cuecount)
cuerate <- unique(wren_cuecount[ , c("Cue.rate","Cue.rate.SE")])
names(cuerate) <- c("rate", "SE")
mult <- list(creation=cuerate)
print(mult)
$creation
    rate     SE
1 1.4558 0.2428
# Search time is the effort - this is 2 * 5min visits
wren_cuecount$Effort <- wren_cuecount$Search.time
w3.hr <- ds(wren_cuecount, transect="point", key="hr", adjustment=NULL, truncation=92.5)

The sampling fraction for these data will be 1 because the full circle around the observer was searched.

conversion.factor <- convert_units("meter", NULL, "hectare")
w3.est <- dht2(w3.hr, flatfile=wren_cuecount, strat_formula=~1,
               multipliers=mult, convert_units=conversion.factor)
# NB "Effort" here is sum(Search.time) in minutes
# NB "CoveredArea" here is pi * w^2 * sum(Search.time)
print(w3.est, report="density")
Density estimates from distance sampling
Stratification : geographical 
Variance       : P2, n/L 
Multipliers    : creation 
Sample fraction : 1 


Summary statistics:
 .Label Area CoveredArea Effort   n  k    ER se.ER cv.ER
  Total 33.2    860.1681    320 765 32 2.391 0.236 0.099

Density estimates:
 .Label Estimate    se  cv    LCI    UCI      df
  Total   1.2092 0.242 0.2 0.8195 1.7843 522.541

Component percentages of variance:
 .Label Detection    ER Multipliers
  Total      6.14 24.33       69.54

Note the large proportion of the uncertainty in winter wren density stems from variability in cue (song) rate. Analyses of the cue count data are necessarily rather subjective as the data show substantial over-dispersion (a single bird may give many song bursts all from the same location during a five minute count). In this circumstance, goodness-of-fit tests are misleading and care must be taken not to over-fit the data (i.e. fit a complicated detection function).

plot(w3.hr, pdf=TRUE, main="Cue distances of winter wren.")
gof_ds(w3.hr)


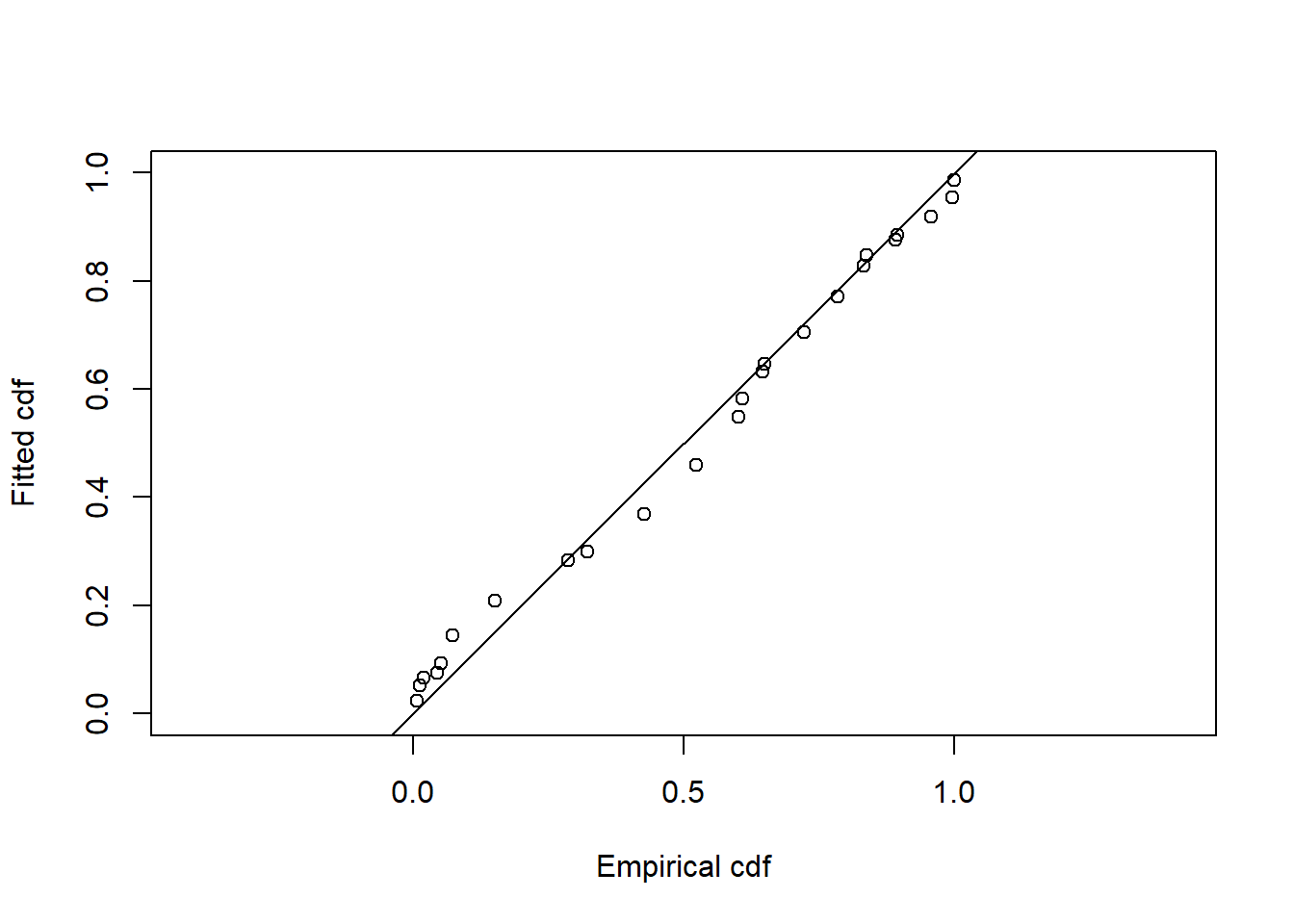
Goodness of fit results for ddf object

Distance sampling Cramer-von Mises test (unweighted)
Test statistic = 1.70062 p-value = 6.04794e-05

References

Buckland, S. T. (2006). Point-transect surveys for songbirds: Robust methodologies. The Auk, 123(2), 345–357. https://doi.org/10.1642/0004-8038(2006)123[345:PSFSRM]2.0.CO;2
Laing, S. E., Buckland, S. T., Burn, R. W., Lambie, D., & Amphlett, A. (2003). Dung and nest surveys: Estimating decay rate. Journal of Applied Ecology, 40, 1102–1111. https://doi.org/10.1111/j.1365-2664.2003.00861.x
Marques, F. F. C., Buckland, S. T., Goffin, D., Dixon, C. E., Borchers, D. L., Mayle, B. A., & Peace, A. J. (2001). Estimating deer abundance from line transect surveys of dung: sika deer in southern Scotland. Journal of Applied Ecology, 38(2), 349–363. https://doi.org/10.1046/j.1365-2664.2001.00584.x